O colesterol LDL (cLDL) é essencial na abordagem do risco de doenças cardiovasculares. Desde 1972 é utilizada a fórmula de Friedewald para estimativa da concentração do cLDL, com algumas limitações. Foi sugerida, em 2013, por Martin et al., uma fórmula semelhante que permite melhor exatidão no cálculo do cLDL.
ObjetivoMostrar aplicabilidade da nova fórmula, que nomeámos fórmula Martin‐Hopkins, na população portuguesa e comparar com a fórmula Friedewald utilizando o cLDL direto.
Material e métodosEstudo transversal, incluindo 1689 participantes do estudo e_COR. Aplicámos as fórmulas Martin‐Hopkins e Friedewald para a estimativa de cLDL (cLDL‐M e cLDL‐F). A fórmula Friedewald não foi aplicada em 12 casos por triglicéridos ≥ 400mg/dL. Foi realizada a determinação direta do cLDL (cLDL‐D). Resultados apresentados em mediana e amplitude interquartil. Nível de significância aceite p < 0,05.
ResultadosDos participantes, 50,2% eram sexo masculino e mediana de 51 (34) anos. O cLDL‐D foi 117,0 (44,0) mg/dL, cLDL‐M foi 114,6 (43,7) mg/dL e cLDL‐F foi 113,8 (43,2) mg/dL. O coeficiente de Spearman (ρ) entre cLDL‐M/cLDL‐D foi 0,987 e entre cLDL‐F/cLDL‐D foi 0,983, p = 0,001. Esta forte correlação manteve‐se no grupo com diabetes mellitus (cLDL‐M/LDL‐D ρ = 0,987; cLDL‐F/cLDL‐D ρ = 0,978, p = 0,001) e hipertrigliceridemia (cLDL‐M/LDL‐D ρ = 0,983; cLDL‐F/cLDL‐D ρ = 0,982, p = 0,001). Na análise de concordância, o maior valor de κ = 0,90 foi obtido para cLDL‐M quando cLDL‐D < 100mg/dL.
ConclusãoA fórmula Martin‐Hopkins teve um bom desempenho e aplicabilidade, mostrando superioridade em relação à fórmula Friedewald, sobretudo para valores de cLDL‐D < 100mg/dL, diabetes mellitus e hipertrigliceridemia.
Low‐density lipoprotein cholesterol (LDL) is essential in managing cardiovascular disease risk. Since 1972, the Friedewald formula has been used to estimate LDL concentration, although with some limitations. In 2013, Martin et al. proposed a similar but more accurate formula for calculating LDL.
AimTo assess the applicability of the new formula, which we have named the Martin‐Hopkins formula, in the Portuguese population and compare it with the Friedewald formula using direct LDL.
Material and methodsCross‐sectional study, including 1689 participants from the e_COR study. We applied the Martin‐Hopkins and Friedewald formulas for estimated LDL (LDL‐M and LDL‐F). The Friedewald formula was not applied in 12 cases due to triglycerides ≥400mg/dL. Direct LDL was measured and the accepted significance level was p<0.05.
ResultsOf the total subjects, 50.2% were male and had a median age of 51 (34) years. LDL‐D was 117.0 (44.0) mg/dL, LDL‐M was 114.6 (43.7) mg/dL and LDL‐F was 113.8 (43.2) mg/dL. The Spearman coefficient (ρ) between LDL‐M/LDL‐D was 0.987 and between LDL‐F/LDL‐D was 0.983, p=0.001. This strong correlation was maintained in the group with diabetes (LDL‐M/LDL‐D ρ=0.987; LDL‐F/LDL‐D ρ=0.978, p=0.001) and hypertriglyceridemia (LDL‐M/LDL‐D ρ=0.983; LDL‐F/LDL‐D ρ=0.982, p=0.001). In terms of agreement, the highest value of κ=0.90 was obtained for LDL‐M when LDL‐D <100 mg/dL.
ConclusionThe Martin‐Hopkins formula performed well and had good applicability, showing superiority in relation to the Friedewald formula, especially for LDL‐D values <100 mg/dL, diabetes, and hypertriglyceridemia.
A doença cardiovascular aterosclerótica é uma das principais causas de morbilidade e mortalidade em Portugal.1
O colesterol presente na lipoproteína de baixa densidade (cLDL) está associado à formação de placas ateroscleróticas e é um importante fator de risco modificável para doença cardiovascular, sendo utilizado como alvo terapêutico primário em recomendações nacionais e internacionais.2–4 O estudo Disgen‐Lipid, observacional de 24 centros de Portugal, mostrou que o atingimento dos valores‐alvo do cLDL foi subótimo e que é necessária uma abordagem mais vigorosa deste fator de risco.5 De acordo com as recomendações da Sociedade Europeia de Cardiologia (ESC) e da Sociedade Europeia de Aterosclerose (EAS), os objetivos do cLDL para as diferentes categorias de risco são redução ≥ 50% do valor basal e um valor alvo de < 55mg/dL se risco muito alto (grau I, nível de evidência C), redução ≥ 50% do valor basal e um valor alvo de < 70mg/dL se risco alto (grau I, nível de evidência A), < 100mg/dL se risco moderado (grau IIa, nível de evidência A) e < 116mg/dL se risco baixo (grau IIb, nível de evidência A).3
O método de referência para a determinação do cLDL é a ultracentrifugação e precipitação química (quantificação β), um processo moroso, dispendioso e pouco viável na prática clínica. Apesar da existência de vários métodos para a determinação direta da concentração de LDL, muitos laboratórios clínicos utilizam a estimativa do cLDL pela simplicidade e ausência de custos, sendo a fórmula de Friedewald a mais amplamente usada.3
A equação de Friedewald baseia‐se na subtração do colesterol não HDL pela variação de VLDL numa relação de 1:5 de acordo com os triglicéridos (Tgs) e é utilizada na prática clínica desde 1972. Esta proporção fixa pode levar a incorreções na estimativa de cLDL que poderão ter impacto na clínica e em decisões terapêuticas. Foi salientado pelo próprio autor que a simples divisão dos triglicéridos por cinco não permite uma estimativa precisa da concentração de VLDL e em várias circunstâncias, como Tgs acima de 400mg/dL e disbetalipoproteinemias, esta fórmula não pode ser aplicada.4,6
Vários estudos têm descrito a tendência da fórmula de Friedewald de subestimar os resultados do cLDL sobretudo naqueles com hipertrigliceridemia (Tgs ≥ 150mg/dL), diabetes mellitus, doença hepática alcoólica e doença renal crónica em diálise.7–11 A subestimação pode ser problemática, podendo levar à protelação de cuidados preventivos e terapêuticos.7,11 Por esta razão, vários investigadores têm tentado modificar o rácio dos Tgs:VLDL de forma a tornar a fórmula mais precisa e exata. Em 2013, Martin et al12 sugeriram uma fórmula semelhante à de Friedewald, em que a estimativa do colesterol VLDL é calculada pela divisão dos Tgs por um fator ajustável que depende do valor do colesterol não HDL e dos Tgs (Anexo 1). Estudos de validação têm mostrado a sua superioridade à fórmula original de Friedewald na estimativa da concentração do cLDL em várias populações.11,13–15
Assim, os objetivos do nosso trabalho foram mostrar a aplicabilidade da nova fórmula, que nomeámos fórmula de Martin‐Hopkins, numa amostra da população portuguesa, comparar com a fórmula de Friedewald e determinar qual se aproxima mais do cLDL determinado por método laboratorial direto.
Material e métodosPopulação do estudoForam incluídos 1689 participantes do estudo e_COR, que decorreu entre 2012 e 2014. O estudo e_COR foi populacional com componente laboratorial numa amostra aleatória e estratificada por género e idade, das cinco regiões de Portugal continental, com o objetivo de obter dados representativos dos principais fatores de risco cardiovascular na população portuguesa.16 O estudo e_COR foi aprovado pela Comissão de Ética do Instituto Nacional de Saúde Doutor Ricardo Jorge e pela Comissão Nacional de Proteção de Dados. Todos os procedimentos foram realizados de acordo com as boas práticas da Declaração de Helsínquia, com a explicação e o preenchimento de consentimento informado.
Avaliações clínicasTodos os participantes completaram um questionário que incluía dados demográficos, história pessoal e familiar, medicação habitual e hábitos comportamentais. Foi avaliada a pressão arterial (em mmHg), o peso (em kg), a altura (em cm) e o perímetro da cintura (em cm).
Avaliações laboratoriaisAs análises de sangue foram obtidas após jejum de 12 horas e foram determinados vários parâmetros bioquímicos. A concentração do cLDL foi determinada pelo método colorimétrico direto no equipamento Cobas Integra® 400da Roche.
Aplicamos as fórmulas de Martin‐Hopkins e Friedewald para a estimativa de cLDL (Anexo 1). A fórmula de Friedewald não foi aplicada em 12 casos por triglicéridos ≥ 400mg/dL.
Análise estatísticaOs resultados são apresentados em mediana e amplitude interquartil (mediana [IQR]). Dividimos a população do estudo em seis grupos para melhor caracterização das correlações e medianas segundo diferentes condições (Anexo 2). Para a correlação entre o colesterol LDL direto (cLDL‐D), colesterol LDL estimado pela fórmula de Friedewald (cLDL‐F) e colesterol LDL estimado pela fórmula de Martin‐Hopkins (cLDL‐M) utilizou‐se o coeficiente de correlação ρ de Spearman e a regressão linear (R2). Para avaliar as diferenças das medianas do cLDL‐F e cLDL‐M com o cLDL‐D recorreu‐se ao teste de Wilcoxon. Na análise da concordância do cLDL‐F e cLDL‐M com o cLDL‐D de acordo com alvos terapêuticos das linhas de orientação da ESC/EAS 20193, empregou‐se a estatística kappa de Cohen (κ). O nível de significância aceite foi p < 0,05.
ResultadosA idade mediana da população do estudo (1689 participantes) foi de 51 (34) anos e 50,2% da população eram do sexo masculino. O IMC foi de 27,0 (5,7) kg/m2 no sexo masculino e 25,8 (6,7) kg/m2 no sexo feminino (Tabela 1). Foi também calculada para todos os participantes a massa de gordura relativa (Relative Fat Mass – RFM). A hipertensão arterial (HTA), a obesidade e diabetes mellitus (DM) estavam presentes em 48,5%, 22,6% e 11,7% da população do estudo. Estavam sob terapêutica antidislipidémica 28,1% (n = 474) dos participantes.
Dados demográficos e prevalência de certas condições na amostra
| Idade (anos)a | 51 (34) |
| Mínimo | 18 |
| Máximo | 79 |
| Sexo (n, %) | |
| Masculino | 848 (50,2%) |
| Feminino | 841 (49,8%) |
| IMC (kg/m2)a | |
| Masculino | 27,0 (5,7) |
| Feminino | 25,8 (6,7) |
| RFM (%)a,b | |
| Masculino | 28,6 (6,6) |
| Feminino | 40,8 (8,2) |
| HTA | 820 (48,5%) |
| Obesidadec | 382 (22,6%) |
| Diabetes mellitus | 198 (11,7%) |
| História de EAM | 42 (2,5%) |
| Sob terapêutica para hipercolesterolemia | 454 (26,9%) |
| Sob terapêutica para hipertrigliceridemia | 45 (2,7%) |
EAM, enfarte agudo do miocárdio. HTA, hipertensão arterial. IMC, índice de massa corporal. RFM, massa gorda relativa.
Massa gorda relativa (Relative Fat Mass17) obtido através da equação 64 ‐ (20×altura[m]/cintura[m]) + (12×sexo[0 se ♂; 1 se ♀]), os pontos de corte para obesidade são ≥ 22,8% ♂ e ≥ 33,9% ♀.
O colesterol total e o colesterol HDL tiveram como mediana 192 (48) e 54 (20) mg/dL, respetivamente (Tabela 2). A mediana do colesterol LDL direto (cLDL‐D) foi 117,0 (44,0) mg/dL; a mediana do colesterol estimado cLDL‐F foi 113,8 (43,2) mg/dL com uma diferença estatisticamente significativa de ‐3,1mg/dL (IC 95%: ‐3,3 a ‐2,8, p < 0,001) em relação ao cLDL‐D; a mediana do colesterol estimado cLDL‐M foi 114,6 (43,7) mg/dL com uma diferença estatisticamente significativa de ‐2,8mg/dL (IC 95%: ‐3,1 a ‐2,6, p < 0,001) em relação ao cLDL‐D. Em relação ao fator usado para o cálculo do cLDL‐M a mediana foi de 4,8 (1,1). A mediana do colesterol não HDL e dos triglicéridos foi 135 (50) mg/dL e 94 (60) mg/dL, respetivamente. Na amostra, 12 participantes (0,7%) apresentaram triglicéridos ≥ 400mg/dL.
Parâmetros clínicos e analíticos avaliados na amostra e colesterol LDL calculado pelas fórmulas de Friedewald e de Martin‐Hopkins
| Parâmetros | Mediana (IQR) |
|---|---|
| Pressão arterial sistólica (mmHg) | 126,5 (31) |
| Pressão arterial diastólica (mmHg) | 79,5 (15,5) |
| Glicémia população do estudo (mg/dL) | 91,0 (17) |
| Glicémia nos diabéticos (mg/dL) | 135 (41) |
| HbA1c população do estudo (%) | 5,4 (0,5) |
| HbA1c nos diabéticos (%) | 7,0 (1,0) |
| Creatinina (mg/dL) | 0,75 (0,23) |
| Colesterol total (mg/dL) | 192 (48) |
| Colesterol HDL (mg/dL) | 54 (20) |
| Colesterol LDL (direto) (mg/dL) | 117 (44) |
| Colesterol LDL (Friedewald) (mg/dL) | 114 (43) |
| Colesterol LDL (Martin‐Hopkins) (mg/dL) | 115 (44) |
| Colesterol não‐HDL (mg/dL) | 135 (50) |
| Triglicéridos (mg/dL) | 94 (60) |
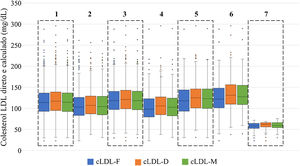
A distribuição dos valores do cLDL direto e calculado para a população do estudo e para os diferentes grupos (sob terapêutica antidislipidémica, sem terapêutica antidislipidémica, diabetes mellitus, obesidade, hipertrigliceridemia e cLDL‐D < 70mg/dL) está representada na Figura 1. Para os vários grupos foram calculadas a mediana e a diferença entre medianas do colesterol direto e calculado (Tabela 3). Para todos os grupos foi possível verificar valores calculados pela fórmula de Friedewald mais baixos e diferenças maiores entre as medianas do cLDL‐F e cLDL‐D. No grupo com cLDL‐D < 70mg/dL foi encontrada uma diferença não significativa de ‐0,95 (IC 95%: ‐2,1 a 0,2, p = 0,117) entre os valores calculados pela fórmula de Martin‐Hopkins e o colesterol LDL direto.
Diagramas de caixas para comparação das medianas e amplitude interquartil do colesterol direto e calculado na população do estudo e nos vários grupos. 1 ‐ Comparação na população do estudo (n = 1677/n = 1689). 2 ‐ Comparação no grupo sob terapêutica antidislipidémica (n = 470/n = 474). 3 ‐ Comparação no grupo sem terapêutica antidislipidémica (n = 1.207/n = 1.215). 4 ‐ Comparação no grupo com diabetes mellitus (n = 192/n = 198). 5 ‐ Comparação no grupo com obesidade (n = 373/n = 382). 6 ‐ Comparação no grupo com hipertrigliceridémia (TGs ≥ 150 e < 400mg/dL) (n = 276). 7 – Comparação no grupo com cLDL‐D < 70mg/dL (n = 82/84). cLD‐D, colesterol LDL direto. cLDL‐F, colesterol LDL calculado pela fórmula de Friedewald. cLDL‐M, colesterol LDL calculado pela fórmula de Martin‐Hopkins.
Diferença entre as medianas do colesterol calculado e direto nos vários grupos da população do estudo que foram definidos segundo dados adquiridos no estudo e_COR
| cLDL‐D, mg/dL | cLDL‐F, mg/dL | cLDL‐M, mg/dL | |||||
|---|---|---|---|---|---|---|---|
| Grupo | Mediana (IQR) | Mediana(IQR) | dif(IC 95%)a | p‐value | Mediana(IQR) | dif(IC 95%)b | p‐value |
| “Sob terapêutica antidislipidémica” | 107,0 (42,0) | 103,0 (43,0) | ‐3,5 (‐4,5 a ‐3,0) | < 0,001 | 104,1 (43,9) | ‐2,4 (‐2,9 a ‐1,9) | < 0,001 |
| “Sem terapêutica antidislipidémica” | 121,0 (44,0) | 118,0 (43,0) | ‐2,5 (‐3,0 a ‐2,5) | < 0,001 | 118,3 (43,6) | ‐3,0 (‐3,4 a ‐2,8) | < 0,001 |
| Diabetes mellitus | 106,0 (42,0) | 98,0(44,0) | ‐5,0 (‐6,0 a ‐4,0) | < 0,001 | 102,6 (41,8) | ‐2,0 (‐2,8 a ‐1,3) | < 0,001 |
| Obesidade | 125,0 (45,0) | 118,0 (50,0) | ‐4,5 (‐5,5 a ‐4,0) | < 0,001 | 123,0 (46,3) | ‐2,4 (‐2,9 a ‐1,8) | < 0,001 |
| Hipertrigliceridemia | 131,0 (46,0) | 122,0 (47,0) | ‐9,0 (‐10,0 a ‐8,5) | < 0,001 | 127,7 (45,4) | ‐2,2 (‐3,0 a ‐1,5) | < 0,001 |
| cLDL‐D < 70 mg/dL | 62,0 (10,0) | 58,3 (11,9) | ‐2,2 (‐3,3 a ‐1,2) | < 0,001 | 59,4 (11,8) | ‐1,0 (‐2,1 a 0,2) | 0,117 |
cLDL‐D, colesterol LDL direto; cLDL‐F, colesterol LDL calculado pela fórmula de Friedewald; cLDL‐M, colesterol LDL calculado pela fórmula de Martin‐Hopkins. Dif, diferença entre medianas. IC, intervalo de confiança. IQR, amplitude interquartil.
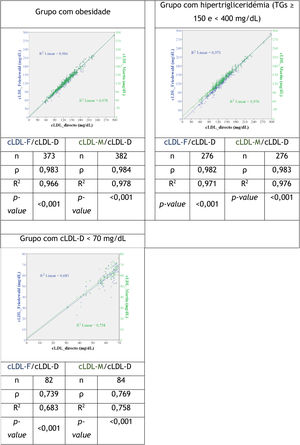
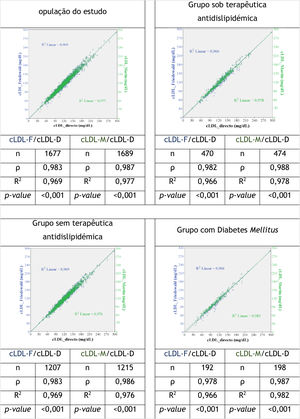
Quando avaliamos a correlação entre as variáveis cLDL‐F/cLDL‐D e cLDL‐M/cLDL‐D na população do estudo e nos diferentes grupos verificou‐se que em todos os casos as correlações são estatisticamente significativas (Figura 2) e com valores superiores na correlação cLDL‐M/cLDL‐D. Estes valores foram muito próximos de 1 na população do estudo e em cinco grupos avaliados: sob terapêutica antidislipidémica, sem terapêutica antidislipidémica, diabetes mellitus, obesidade e hipertrigliceridemia (valores de ρ de Spearman para cLDL‐F/cLDL‐D entre 0,978 e 0,983 e R2 entre 0,966 e 0,971; para cLDL‐M/cLDL‐D os valores de ρ foram entre 0,983 e 0,988 e R2 entre 0,976 e 0,982). No grupo com colesterol cLDL‐D < 70mg/dL, a correlação ρ e R2 foi inferior, embora mostrando superioridade para a fórmula de Martin‐Hopkins (ρ (cLDL‐F/cLDL‐D) = 0,739, R2 (cLDL‐F/cLDL‐D) = 0,683; ρ (cLDL‐M/cLDL‐D) = 0,769, R2 (cLDL‐M/cLDL‐D) = 0,758).
Gráficos de dispersão relacionando o cLDL‐D, cLDL‐F e o cLDL‐M e o coeficiente de correlação entre estas variáveis na população do estudo e nos vários grupos. cLD‐D, colesterol LDL direto. cLDL‐F, colesterol LDL calculado pela fórmula de Friedewald. cLDL‐M, colesterol LDL calculado pela fórmula de Martin‐Hopkins. ρ, coeficiente de correlação ρ de Spearman. R2, regressão linear.
,A concordância do colesterol LDL calculado e direto foi realizada tendo em conta os alvos terapêuticos de acordo com as linhas de orientação da ESC/EAS 2019 (LDL < 55, < 70, < 100, < 116mg/dL)3. O número de casos estimados corretamente com valores abaixo destes alvos foi semelhante entre ambas as fórmulas (Tabela 4). A maior diferença percentual entre a concordância dos casos foi a favor da fórmula de Martin‐Hopkins quando valores de cLDL‐D < 55mg/dL (a fórmula de Friedewald classificou corretamente 75,0% [IC 95% 50,5‐89,8 versus a fórmula de Martin‐Hopkins, que classificou corretamente 87,5% [IC 95% 63,9‐96,5] dos participantes neste alvo). Nos outros alvos terapêuticos verificou‐se concordância superior a 90% para as duas fórmulas. O valor de kappa mostrou concordância «excelente» (ou seja, intervalo entre 0,81 a 1) nos níveis < 70, < 100 e < 116mg/dL para ambas as fórmulas. Na categoria < 100mg/dL foi obtido o maior valor de κ = 0,90 para a concordância entre o cLDL‐M e o cLDL‐D. Em todos os casos a concordância teve significância estatística (p < 0,001).
Concordância entre o colesterol calculado e direto segundo os alvos terapêuticos para as categorias de risco cardiovascular segundo as linhas de orientação da ESC/EAS 20193
| cLDL‐F | cLDL‐M | |||||||
|---|---|---|---|---|---|---|---|---|
| cLDL‐D, mg/dL | F/Da | % (IC 95%) | κc | p‐valor | M/Db | % (IC 95%) | κc | p‐valor |
| < 116 | 796/817 | 97,4 (96,1‐98,3) | 0,89 | < 0,001 | 795/817 | 97,3 (96,0‐98,2) | 0,89 | < 0,001 |
| < 100 | 486/503 | 96,6 (94,7‐97,9) | 0,88 | < 0,001 | 491/503 | 97,6 (95,9‐98,6) | 0,90 | < 0,001 |
| < 70 | 76/84 | 90,5 (82,3‐95,1) | 0,81 | < 0,001 | 77/84 | 91,7 (83,9‐95,9) | 0,86 | < 0,001 |
| < 55 | 12/16 | 75,0 (50,5‐89,8) | 0,53 | < 0,001 | 14/16 | 87,5 (63,9‐96,5) | 0,75 | < 0,001 |
cLDL‐D, colesterol LDL direto; cLDL‐F, colesterol LDL calculado pela fórmula de Friedewald; cLDL‐M, colesterol LDL calculado pela fórmula de Martin‐Hopkins. IC, intervalo de confiança.
Quando avaliámos a discordância entre o colesterol calculado e direto para os alvos terapêuticos de risco muito alto e alto, o cLDL‐F categorizou 60,0% (n = 18) dos casos de cLDL‐D > 55mg/dL (n = 30) como dentro do alvo LDL < 55mg/dL e 29,0% (n = 31) dos casos de cLDL‐D > 70mg/dL (n = 107) como dentro do alvo LDL < 70mg/dL. Para o cLDL‐M, a percentagem de discordância foi 36,4% (n = 8/n = 22) e 25,2% (n = 26/n =103), respetivamente.
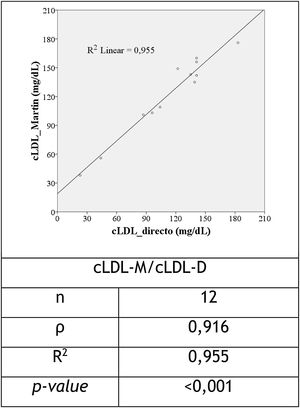
Para os 12 casos nos quais não foi aplicada a fórmula de Friedewald (triglicéridos ≥ 400mg/dL), verificou‐se, como mostrado na Figura 3, que a correlação entre o cLDL‐M e o cLDL‐D foi forte e com significância estatística (ρ = 0,916 e R2 = 0,955, p < 0,001).
DiscussãoO colesterol LDL é um alvo terapêutico primário na prevenção das doenças cardiovasculares (DCV).2–4 Para esse fim é necessária acurácia na sua determinação. O método de referência para o doseamento do cLDL é dispendioso e inviável na prática clínica. Assim, pela sua simplicidade é utilizada há cerca de três décadas a estimativa da concentração de cLDL pela fórmula de Friedewald, que tem sido refutada devido à sua menor acurácia em situações clínicas como a hipertrigliceridemia e a diabetes mellitus. O objetivo do presente trabalho foi aplicar uma nova fórmula que utiliza um rácio Tgs:VLDL variável (Anexo 1) numa amostra da população portuguesa de um estudo nacional, o estudo e_COR, da responsabilidade do Instituto Ricardo Jorge, que decorreu entre 2012 e 2014.16 Esta nova fórmula (classificada como fórmula de Martin‐Hopkins) tem mostrado acurácia superior à de Friedewald em várias populações11–13.
No presente estudo, a amostra em termos descritivos apresenta uma prevalência dos sexos semelhante (50,2% masculino e 49,8% feminino), com idades entre 18 e 79, com uma mediana de 51 (34) anos. A mediana do IMC correspondeu a “excesso de peso” nos dois sexos (IMC de 27,0 [5,7] kg/m2 no sexo masculino e 25,8 [6,7] kg/m2 no feminino) e a mediana da massa de gordura relativa (Relative Fat Mass – RFM15) correspondeu a “obesidade” (RFM de 28,6 [6,6]% no sexo masculino e 40,8 [8,2]% no sexo feminino). O RFM é um parâmetro que utiliza o perímetro da cintura em vez do peso para definir obesidade, sendo comprovada em vários estudos a sua utilidade relativamente ao IMC, com pontos de corte a serem definidos e validados consoante o tipo de população/etnia.17,18
Em relação aos fatores de risco para DCV, verificou‐se que quase metade dos participantes apresentava HTA (48,5%). A obesidade estava presente em 22,6% e a diabetes mellitus em 11,7% da amostra, aproximando‐se da prevalência de DM em 2012 de 12,9% na população portuguesa.19 No entanto, a prevalência de DM na nossa amostra não foi ajustada à população portuguesa, que, de acordo com o relatório do estudo e_COR, foi de 8,9% (IC 95%: 7,5‐10,3).16 Mais de um quarto da nossa amostra estava sob estatinas (26,9%), o que mostra a ampla utilização destes fármacos em Portugal.20
A mediana dos valores doseados diretamente (cLDL‐D) foi superior à mediana dos valores estimados (cLDL‐F e cLDL‐M) na população do estudo, com diferença entre medianas estatisticamente significativa para os valores calculados pela fórmula de Friedewald de ‐3,1mg/dL (IC 95%: ‐3,3 a ‐2,8, p < 0,001) e para aqueles calculados pela fórmula de Martin‐Hopkins de ‐2,8mg/dL (IC 95%: ‐3,1 a ‐2,6, p < 0,001). Apesar de um coeficiente de correlação forte, houve dissemelhanças diferentes de zero em relação à determinação direta do cLDL para ambas as fórmulas. As diferenças encontradas na população do estudo foram inferiores ao relatado noutros estudos e em outras populações.11,15 A mediana do rácio Tgs:VLDL para o cálculo do cLDL‐M foi de 4,8 (1,1), aproximando‐se ao encontrado por Sathiyakumar et al.21 de 4,9 (4,3‐5,7). Este estudo avaliou o desempenho da fórmula de Martin‐Hopkins versus a fórmula de Friedewald no estado de jejum e pós‐prandial, mostrando superioridade da fórmula de Martin‐Hopkins nos dois estados. Em comparação com o estudo de Martin et al.,12 o nosso rácio foi inferior ao relatado de 5,2 (4,5‐6,0), sendo um fator dependente da composição da população em análise. No entanto, os rácios descritos são próximos de 5, o que explica a semelhança no desempenho entre fórmulas no presente e nos estudos anteriormente referidos, com superioridade em todos os casos para a fórmula de Martin‐Hopkins.
De acordo com estudos anteriores, a tendência de subestimar os valores de cLDL pela fórmula de Friedewald ocorre sobretudo na presença de DM, hipertrigliceridemia e cLDL < 70mg/dL.7,9,22,23 No nosso estudo verificámos a tendência para ambas as fórmulas de subestimar os valores de cLDL na população do estudo e nos grupos definidos (Figura 1 e Tabela 3). A mediana de cLDL‐D mais elevada foi no grupo com hipertrigliceridemia (cLDL‐D de 131,0 [46,0] mg/dL), sendo neste grupo encontrada a diferença mais significativa entre as medianas de cLDL‐F e o cLDL‐D de ‐9,0mg/dL (IC 95%: ‐10,0 a ‐8,5, p < 0,001). No grupo com DM a diferença entre os valores de cLDL‐F e o cLDL‐D também foi expressiva de ‐5,0 (IC 95%: ‐6,0 a ‐4,0, p < 0,001). Notavelmente, os valores de cLDL‐M estiveram mais próximos do cLDL‐D nestes dois grupos: ‐2,2 (IC 95%: ‐3,0 a ‐1,5, p < 0,001) para o grupo com hipertrigliceridemia e ‐2,0 (IC 95%: ‐2,8 a ‐1,3, p < 0,001) para o grupo com DM. Estes resultados mostram a tendência da fórmula de Friedewald de subestimar os valores de cLDL quando estas condições estão presentes e será nestas condições clínicas que a fórmula de Martin‐Hopkins poderá ter mais utilidade.9,24,25
Quando avaliámos os coeficientes da correlação ρ de Spearman e a regressão linear por grupos verificámos que em todos os casos estes foram superiores para os valores calculados pela fórmula de Martin‐Hopkins em comparação com a fórmula de Friedewald, variando os valores de cLDL‐M de forma quase perfeita com os valores de cLDL‐D nos grupos sob terapêutica antidislipidémica, sem terapêutica antidislipidémica, obesidade, diabetes mellitus e hipertrigliceridemia, mostrando uma correlação forte com os valores de cLDL‐D (Figura 2). Para os valores de cLDL‐F os coeficientes de correlação e regressão linear mostraram também uma forte aproximação com a variação dos valores determinados de cLDL‐D.
Para o cLDL‐D < 70mg/dL, alvo terapêutico de grau I e nível de evidência A para indivíduos de alto risco de DCV,3 descrito noutros estudos como ponto de menor acurácia da fórmula de Friedewald, 8,11,13,15,22,23 foi possível verificar uma correlação mais fraca em comparação com outros grupos para ambas as fórmulas, com superioridade para a fórmula de Martin‐Hopkins (Figura 2). A mediana de valores do cLDL‐M neste grupo foi muito próxima da mediana do cLDL‐D, com uma diferença não significativa de ‐0,95 (IC 95%: ‐2,1 a 0,2, p = 0,117), mostrando a superioridade da fórmula de Martin‐Hopkins neste intervalo de valores, o que também foi validado em outros estudos.11,13,21,24
Em relação à concordância do cLDL‐M e do cLDL‐F com o cLDL‐D nos alvos terapêuticos recomendados pela ESC/EAS 2019,3 a exatidão foi menor à medida que o valor de cLDL‐D diminuiu para ambas as fórmulas. No entanto, verificou‐se superioridade para a fórmula de Martin‐Hopkins nos três primeiros alvos (cLDL‐D < 55, < 70, < 100mg/dL) e o maior valor de κ = 0,90 para cLDL‐M quando cLDL‐D < 100mg/dL, o que poderá permitir uma maior confiança quando avaliámos o perfil lipídico de indivíduos de muito alto, alto e moderado risco, em que estes objetivos são importantes de atingir, estando em consonância com o encontrado no estudo original e num estudo populacional de validação desta fórmula.12,13 Em relação aos valores < 116mg/dL, tal como encontrado noutro estudo,15 o cLDL‐F foi marginalmente mais concordante em comparação com o cLDL‐M (97,4% [IC 95%: 96,1‐98,3%] vs. 97,3% [IC 95%: 96,0‐98,2%]).
Quando avaliámos a discordância entre os valores calculados e o cLDL‐D, foi possível verificar que pela fórmula de Friedewald 60,0% e 29,0% dos participantes estariam dentro do alvo terapêutico do muito alto e alto risco, o que implicaria, hipoteticamente, um menor aprimoramento terapêutica nestes casos. No caso da fórmula de Martin‐Hopkins foram encontradas discrepâncias menores, o que tem sido encontrado noutros estudos.26,27 No estudo de Palmer et al.26 e Martin et al27, a nova fórmula permitiu uma estimativa mais alta dos valores de cLDL em relação à fórmula de Friedewald, particularmente nos doentes com baixos níveis de cLDL, sendo salientado que o método de Martin‐Hopkins pode prevenir o subtratamento devido à subestimação do cLDL pelo método de Friedewald nesta faixa de valores.
Apesar de ser um pequeno grupo de indivíduos com Tgs acima ou igual a 400mg/dL (n = 12), o coeficente ρ e R2 encontrado foi forte (> 0,9) e significativo (p < 0,001). Estes resultados não foram encontrados por Palmer et al.,26 em que o novo método de cálculo do cLDL foi impreciso nos doentes com Tgs ≥ 400mg/dL quando comparado com a determinação do cLDL por quantificação β. No entanto, serão necessários mais estudos para comprovar estes dados.
Resumidamente, foram encontrados coeficientes de correlação e regressão linear superiores, maior concordância e diferenças menores entre os valores de cLDL‐M e cLDL‐D em comparação com os valores de cLDL‐F, sobretudo nos grupos definidos com DM, hipertrigliceridemia, cLDL‐D < 70 e < 100mg/dL, sendo claro que o uso desta nova fórmula para estimar o cLDL é uma melhoria em relação à fórmula mais amplamente usada de Friedewald. De acordo com o descrito por Martin et al.,12 alterar um cálculo é uma questão simples num laboratório moderno, podendo ser facilmente incorporado nos sistemas de relatórios laboratoriais automatizados praticamente sem custo adicional. As 180 células estratificadas (Anexo 1) podem ser adicionadas através de um software disponível on‐line (http://ldlcalculator.com/) e, assim, facilmente implantado na maioria dos laboratórios clínicos. Apesar de ser uma fórmula que implica a consulta de uma tabela para o divisor variável dos Tgs, na prática clínica existe a possibilidade da utilização de uma aplicação móvel desenvolvida pelo Centro Ciccarone para a Prevenção de Doenças Cardiovasculares do Hospital Johns Hopkins que permite a estimativa do cLDL pelo método de Martin‐Hopkins (https://www.hopkinsmedicine.org/apps/all‐apps/ldl‐cholesterol‐calculator).
É importante também observar que o cLDL na prática clínica é um componente único entre muitos dos fatores que determinam o risco de doença cardiovascular de um indivíduo1–4 e que a utilização do colesterol não HDL como alvo terapêutico permite que interferências no cálculo do cLDL sejam minimizadas na decisão terapêutica, sendo recomendado particularmente em pessoas com altos níveis de Tgs, DM, obesidade ou níveis muito baixos de cLDL (recomendação grau I, nível C).3,24
LimitaçõesUma das limitações deste estudo foi o método de medição direta do cLDL, que não foi o mesmo aplicado por Martin et al.,12 que utilizou a ultracentrifugação direta com perfil automático vertical (VAP; Atherotech), e por Friedewald et al.,6 que utilizou a quantificação β. No entanto, os métodos diretos (ensaios homogéneos de 3.ª geração) para determinação do cLDL mostraram boa reprodutibilidade e certificação pela Rede de Laboratórios de Métodos de Referência para o Colesterol (Cholesterol Reference Methods Laboratory Network – CRMLN) do Centro de Controlo e Prevenção de Doenças (CDC).28
No presente estudo foram avaliadas medições únicas. Portanto, não têm em conta a variação individual dos níveis lipídicos.
Ponto‐forteÉ o primeiro estudo na população portuguesa que mostra a aplicabilidade da fórmula de Martin‐Hopkins em relação à fórmula de Friedewald largamente usada no nosso País.
ConclusãoA fórmula desenvolvida por Martin et al.12 usa um fator ajustável para a relação Tgs/VLDL, que permite acurácia superior à fórmula mais divulgada de Friedewald na estimativa da concentração do cLDL. A aplicação desta nova fórmula é simples e válida e teve um bom desempenho na nossa amostra, mostrando superioridade em relação à fórmula de Friedewald, sobretudo para valores de cLDL‐D < 100mg/dL e nos grupos definidos com diabetes mellitus e hipertrigliceridemia.
FinanciamentoEsta investigação não recebeu financiamento específico de qualquer setor comercial, público ou sem fins lucrativos.
Conflitos de interesseOs autores declaram não haver conflitos de interesses.
Aos participantes, investigadores e técnicos de análises que trabalharam no projeto de investigação do estudo e_COR.