Low-density lipoprotein cholesterol (LDL) is essential in managing cardiovascular disease risk. Since 1972, the Friedewald formula has been used to estimate LDL concentration, although with some limitations. In 2013, Martin et al. proposed a similar but more accurate formula for calculating LDL.
AimTo assess the applicability of the new formula, which we have named the Martin-Hopkins formula, in the Portuguese population and compare it with the Friedewald formula using direct LDL.
MethodsCross-sectional study, including 1689 participants from the e_COR study. We applied the Martin-Hopkins and Friedewald formulas for estimated LDL (LDL-M and LDL-F). The Friedewald formula was not applied in 12 cases due to triglycerides ≥400mg/dL. Direct LDL was measured and the accepted significance level was p<0.05.
ResultsOf the total subjects, 50.2% were male and had a median age of 51 (34) years. LDL-D was 117.0 (44.0) mg/dL, LDL-M was 114.6 (43.7) mg/dL and LDL-F was 113.8 (43.2) mg/dL. The Spearman coefficient (ρ) between LDL-M/LDL-D was 0.987 and between LDL-F/LDL-D was 0.983, p=0.001. This strong correlation was maintained in the group with diabetes (LDL-M/LDL-D ρ=0.987; LDL-F/LDL-D ρ=0.978, p=0.001) and hypertriglyceridemia (LDL-M/LDL-D ρ=0.983; LDL-F/LDL-D ρ=0.982, p=0.001). In terms of agreement, the highest value of κ=0.90 was obtained for LDL-M when LDL-D <100mg/dL.
ConclusionThe Martin-Hopkins formula performed well and had good applicability, showing superiority in relation to the Friedewald formula, especially for LDL-D values <100mg/dL, diabetes, and hypertriglyceridemia.
O colesterol LDL (cLDL) é essencial na abordagem do risco de doenças cardiovasculares. Desde 1972 é utilizada a fórmula de Friedewald para estimativa da concentração do cLDL, com algumas limitações. Foi sugerido, em 2013, por Martin et al. uma fórmula semelhante que permite melhor exatidão no cálculo do cLDL.
ObjetivoMostrar aplicabilidade da nova fórmula, que nomeámos fórmula Martin-Hopkins, na população portuguesa e comparar com a fórmula Friedewald utilizando o cLDL direto.
Materiais e MétodosEstudo transversal, incluído 1689 participantes do estudo e_COR. Aplicamos as fórmulas Martin-Hopkins e Friedewald para a estimativa de cLDL (cLDL-M e cLDL-F). A fórmula Friedewald não foi aplicada em 12 casos por triglicéridos ≥400mg/dL. Foi realizada a determinação direta do cLDL (cLDL-D). Resultados apresentados em mediana e amplitude interquartil. Nível de significância aceite p<0,05.
ResultadosDo total de participantes, 50,2% eram sexo masculino e mediana de 51 (34) anos de idade. O cLDL-D foi 117,0 (44,0) mg/dL, cLDL-M foi 114,6 (43,7) mg/dL e cLDL-F foi 113,8 (43,2) mg/dL. O coeficiente de Spearman (ρ) entre cLDL-M/cLDL-D foi 0,987 e entre cLDL-F/cLDL-D foi 0,983, p=0,001. Esta forte correlação manteve-se no grupo com diabetes mellitus (cLDL-M/LDL-D ρ=0,987; cLDL-F/cLDL-D ρ=0,978, p=0,001) e hipertrigliceridemia (cLDL-M/LDL-D ρ=0,983; cLDL-F/cLDL-D ρ=0,982, p=0,001). Na análise de concordância, o maior valor de κ=0,90 foi obtido para cLDL-M quando cLDL-D <100mg/dL.
ConclusãoA fórmula Martin-Hopkins teve um bom desempenho e aplicabilidade, mostrando superioridade em relação à fórmula Friedewald, sobretudo para valores de cLDL-D <100mg/dL, diabetes mellitus e hipertrigliceridemia.
Atherosclerotic cardiovascular disease (CVD) is a major cause of morbidity and mortality in Portugal.1 Low-density lipoprotein (LDL) cholesterol is associated with atherosclerotic plaque formation and is an important modifiable risk factor for CVD and is used as a primary therapeutic target in national and international recommendations.2–4 The Disgen-Lipid study, an observational study of 24 centers in Portugal, showed that obtaining LDL cholesterol target values was suboptimal and that a stricter approach to this risk factor was needed.5 According to the recommendations of the European Society of Cardiology (ESC) and the European Atherosclerosis Society (EAS), LDL targets for the different risk categories are a ≥50% reduction in the baseline value and a target value of <55mg/dL if very high-risk (grade I, level of evidence C), a reduction ≥50% in the baseline value and a target value of <70mg/dL if high-risk (grade I, level of evidence A), <100mg/dL if moderate risk (grade IIa, level of evidence A), and <116mg/dL if low risk (grade IIb, level of evidence A)3.
The reference method for LDL cholesterol is ultracentrifugation and chemical precipitation (β-precipitation), which is time-consuming, expensive, and not very feasible in clinical practice. Despite the existence of several methods for direct LDL cholesterol concentration analysis, many clinical laboratories use LDL cholesterol estimation for its simplicity and lack of associated costs; Friedewald's formula is the most widely used calculation.3
The Friedewald equation is based on subtracting non-high-density lipoprotein (non-HDL) cholesterol from the variation in very-low-density lipoprotein (VLDL) in a 1:5 ratio according to triglycerides (TG) and has been used in clinical practice since 1972. This fixed ratio can lead to inaccuracies in LDL estimation that may have an impact upon clinical and therapeutic decisions. The author of the formula himself highlighted that simply dividing triglycerides by five does not lead to an accurate estimate of VLDL concentration and in several circumstances, such as TG>400mg/dL and dysbetalipoproteinemia, this formula cannot be applied.4,6
Several studies have described the tendency of the Friedewald formula to underestimate LDL cholesterol especially in patients with hypertriglyceridemia (TG≥150mg/dL), diabetes, alcoholic liver disease, and chronic kidney disease on dialysis.7–11 Underestimation can be problematic and may lead to the postponement of preventive and therapeutic care.7,11 For this reason several investigators have attempted to modify the TG:VLDL ratio to make it more precise. In 2013, Martin et al.12 proposed a formula similar to Friedewald's, in which the estimate of VLDLcholesterol is calculated by dividing TG by an adjustable factor that depends on the non-HDL-cholesterol and TG values (Appendix 1, Supplementary data). Validation studies have shown its superiority to the original Friedewald formula in estimating LDL cholesterol concentration in various populations.11,13–15
The objectives of our research were, thus, to show the applicability of the new formula, which we named Martin-Hopkins formula, to a sample of the Portuguese population, to compare it with Friedewald's formula, and to determine which formula renders a value closer to the LDL cholesterol determined by direct laboratory analysis.
Materials and methodsStudy populationA total of 1689 participants were included in the e_COR study, which took place between 2012 and 2014. The e_COR was a population-based study with a laboratory component in a random sample stratified according to gender and age in the five regions of mainland Portugal. It sought to obtain representative data on the main cardiovascular risk factors in the Portuguese population.16 This study was approved by the Ethics Committee of the Instituto Nacional de Saúde Doutor Ricardo Jorge and by the National Data Protection Committee. All procedures were performed in accordance with Declaration of Helsinki Good Clinical Practice Guidelines; the study was explained to subjects and informed consent was obtained.
Clinical evaluationsAll subjects completed a questionnaire that included demographics, personal and family history, usual medication, and behavioral habits. Blood pressure (in mmHg), weight (in kg), height (in cm), and waist circumference (in cm) were recorded.
Laboratory evaluationsBlood tests were obtained after a 12 hour fasting period and several biochemical parameters were measured. LDL cholesterol concentration was analyzed using the direct colorimetric method in the Cobas Integra 400 equipment from Roche.
We applied the Martin-Hopkins and Friedewald formulas for LDL cholesterol estimation (Appendix 1, Supplementary data). The Friedewald formula was not applied in 12 cases due to TG≥400mg/dL.
Statistical analysisResults are presented as median and interquartile range (IQR). We divided the study population into six groups for better characterization of correlations and medians according to different conditions (Appendix 2, Supplementary data). For the correlation between direct LDL cholesterol (LDL-D cholesterol), LDL cholesterol estimated with the Friedewald formula (LDL-F) and LDL cholesterol estimated with the Martin-Hopkins formula (LDL-M), we used Spearman's rank correlation coefficient and linear regression (R2). Wilcoxon signed-rank test was used to assess the differences between LDL-F and LDL-M medians and LDL-D. Cohen's kappa coefficient (κ) was used to analyze the agreement of LDL-F and LDL-M with LDL-D according to the therapeutic targets of the ESC/EAS 20193 guidelines. The accepted statistical significance was p<0.05.
ResultsThe median age of the study population (1689 subjects) was 51 (34) years and 50.2% of the population was male. Body mass index (BMI) was 27.0 (5.7) kg/m2 in males and 25.8 (6.7) kg/m2 in females (Table 1). Relative fat mass (RFM) was also calculated for all subjects. Hypertension, obesity, and diabetes were present in 48.5%, 22.6% and 11.7% of the study population. A total of 28.1% (n=474) of the subjects were on lipid-lowering therapy.
Demographics and prevalence of certain conditions in the sample.
| Age (years)a | 51 (34) |
| Minimum | 18 |
| Maximum | 79 |
| Gender (n, %) | |
| Male | 848 (50.2%) |
| Female | 841 (49.8%) |
| BMI (kg/m2)a | |
| Male | 27.0 (5,7) |
| Female | 25.8 (6.7) |
| RFM (%)a,b | |
| Male | 28.6 (6.6) |
| Female | 40.8 (8.2) |
| Hypertension | 820 (48.5%) |
| Obesityc | 382 (22.6%) |
| Diabetes | 198 (11.7%) |
| History of AMI | 42 (2.5%) |
| On therapy for hypercholesterolemia | 454 (26.9%) |
| On therapy for hypertriglyceridemia | 45 (2.7%) |
AMI: acute myocardial infarction; BMI: body mass index; RFM: relative fat mass.
Relative fat mass1 obtained from the equation 64 - (20×height(m)/waist(m))+(12×gender (0 if ♂; 1 if ♀)), the cutoff points for obesity are ≥22.8% ♂ and ≥33.9% ♀.
The median total cholesterol and HDL cholesterol were 192 (48) and 54 (20) mg/dL, respectively (Table 2). Median LDL-D cholesterol was 117.0 (44.0) mg/dL; median estimated LDL-F cholesterol was 113.8 (43.2) mg/dL with a statistically significant difference of -3.1mg/dL (95% confidence interval (CI): -3.3 to -2.8, p<0.001) compared to LDL-D; median estimated LDL-M cholesterol was 114.6 (43.7) mg/dL with a statistically significant difference of -2.8mg/dL (95% CI: -3.1 to -2.6, p<0.001) compared to LDL-D. Regarding the factor used to calculate LDL-M, the median was 4.8 (1.1). Median non-HDL-cholesterol and TG levels were 135 (50) mg/dL and 94 (60) mg/dL, respectively. In the sample, we recorded TG≥400mg/dL in 12 subjects (0.7%).
Clinical and laboratory parameters assessed in the sample and calculated LDL cholesterol..
| Parameters | Median (IQR) |
|---|---|
| Systolic blood pressure (mmHg) | 126.5 (31) |
| Diastolic blood pressure (mmHg) | 79.5 (15.5) |
| Glycemia study population (mg/dL) | 91.0 (17) |
| Blood glucose in diabetics (mg/dL) | 135 (41) |
| HbA1c study population (%) | 5.4 (0.5) |
| HbA1c in diabetics (%) | 7.0 (1.0) |
| Creatinine (mg/dL) | 0.75 (0.23) |
| Total Cholesterol (mg/dL) | 192 (48) |
| HDL Cholesterol (mg/dL) | 54 (20) |
| LDL Cholesterol (direct) (mg/dL) | 117 (44) |
| LDL-F (Friedewald) (mg/dL) | 114 (43) |
| LDL-M (Martin-Hopkins) (mg/dL) | 115 (44) |
| Non-HDL-cholesterol (mg/dL) | 135 (50) |
| Triglycerides (mg/dL) | 94 (60) |
HDL: high-density lipoprotein; LDL: low-density lipoprotein.
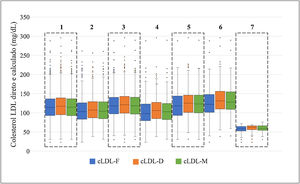
The distribution of direct and calculated LDL cholesterol values among the study population and across the different groups (on lipid-lowering therapy, no lipid-lowering therapy, diabetes, obesity, hypertriglyceridemia, and LDL-D cholesterol <70mg/dL) is shown in Figure 1. Across the various groups, the median and the difference between medians for direct and calculated cholesterol are illustrated in Table 3. In all the groups, the values calculated with the Friedewald formula were lower and there were larger differences between the medians of LDL-F cholesterol and LDL-D cholesterol. In the group with LDL-D cholesterol <70mg/dL, a non-significant difference of -0.95 (95% CI: -2.1 to 0.2, p=0.117) was found between the values calculated with the Martin-Hopkins formula and direct cholesterol.
Box plots to compare the median and interquartile range of direct and calculated cholesterol in the study population and several groups. 1 – Comparison in the study population (n=1677/n=1689). 2 – Comparison in the group under lipid-lowering therapy (n=470/n=474). 3 – Comparison in the group under no lipid-lowering therapy (=1207/n=1215). 4 – Comparison in the group with diabetes (n=192/n=198). 5 – Comparison in the group with obesity (n=373/n=382). 6 – Comparison in the group with LDL-D cholesterol <70mg/dL (n=82/84).
LDL: low-density lipoprotein; LDL-F: low-density lipoprotein cholesterol calculated according to the Friedewald formula; LDL-M: low-density lipoprotein cholesterol calculated according to the Martin-Hopkins formula.
Difference between calculated and direct cholesterol in the groups that were defined according to data acquired in the e_COR study.
| LDL-D, mg/dL | LDL-F, mg/dL | LDL-M, mg/dL | |||||
|---|---|---|---|---|---|---|---|
| Group | Median (IQR) | Median (IQR) | diff (95% CI)a | p-value | Median (IQR) | Diff (95% CI)b | p-value |
| On lipid-lowering therapy | 107.0 (42.0) | 103.0 (43.0) | −3.5 (-4.5 to -3.0) | <0.001 | 104.1 (43.9) | −2.4 (-2.9 to -1.9) | <0.001 |
| No lipid-lowering therapy | 121.0 (44.0) | 118.0 (43.0) | −2.5 (-3.0 to -2.5) | <0.001 | 118.3 (43.6) | −3.0 (-3.4 to -2.8) | <0.001 |
| Diabetes | 106.0 (42.0) | 98.0 (44.0) | −5.0 (-6.0 to -4.0) | <0.001 | 102.6 (41.8) | −2.0 (-2.8 to -1.3) | <0.001 |
| Obesity | 125.0 (45.0) | 118.0 (50.0) | −4.5 (-5.5 to -4.0) | <0.001 | 123.0 (46.3) | −2.4 (-2.9 to -1.8) | <0.001 |
| Hypertriglyceridemia | 131.0 (46.0) | 122.0 (47.0) | −9.0 (-10.0 to -8.5) | <0.001 | 127.7 (45.4) | −2.2 (-3.0 to -1.5) | <0.001 |
| LDL-D <70mg/dL | 62.0 (10.0) | 58.3 (11.9) | −2.2 (-3.3 to -1.2) | <0.001 | 59.4 (11.8) | −1.0 (-2.1 to 0.2) | 0.117 |
CI: confidence interval; LDL-D: direct low-density lipoprotein cholesterol; LDL-F: low-density lipoprotein cholesterol calculated according to the Friedewald formula; LDL-M: low-density lipoprotein cholesterol calculated according to the Martin-Hopkins formula; Diff: difference between medians; CI: confidence interval; IQR: interquartile range;
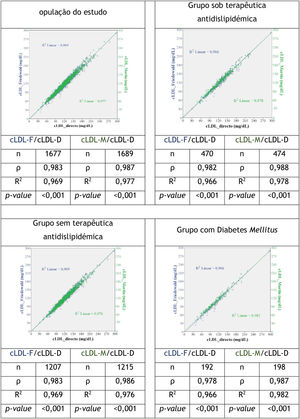
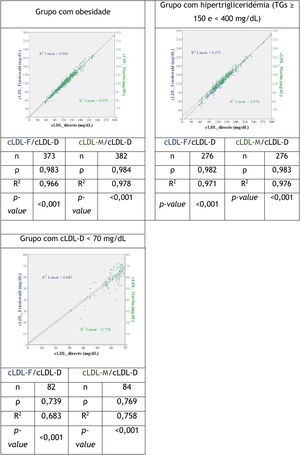
When we assessed the correlation between the variables LDL-F/LDL-D and LDL-M/LDL-D in the study population and in the different groups, it was found that in all cases the correlations were statistically significant (Figure 2); the values in the LDL-M/LDL-D correlation were higher. These values were very close to 1 in the study population and in the five groups under analysis: on lipid lowering therapy, no lipid-lowering therapy, diabetes, obesity and hypertriglyceridemia (Spearman's ρ values for LDL-F/LDL-D between 0.978 and 0.983 and R2 between 0.966 and 0.971; for LDL-M/LDL-D the ρ values were between 0.983 and 0.988 and R2 between 0.976 and 0.982). In the group with LDL-D cholesterol <70mg/dL, the correlation ρ and R2 were lower, although superiority in the case of the Martin-Hopkins formula was demonstrated (ρ (LDL-F/LDL-D)=0.739, R2 (LDL-F/LDL-D)=0.683; ρ (LDL-M/LDL-D)=0.769, R2 (LDL-M/LDL-D)=0.758).
Scatter plots relating LDL-D, LDL-F and LDL-M cholesterol with the coefficient of comparision between these variables in the study population and in the various groups.
LDL-D direct low-density lipoprotein cholesterol; LDL-F: low-density lipoprotein cholesterol calculated according to the Friedewald formula; LDL-M: low-density lipoprotein cholesterol calculated according to the Martin-Hopkins formula; ρ: Spearman’s rank correlation coefficient; R2: linear regression.
Agreement between calculated and direct LDL cholesterol was measured in light of the therapeutic targets outlined in the ESC/EAS 2019 guidelines (LDL<55, <70, <100, <116mg/dL)3. The number of correctly estimated cases with values below these targets was similar between both formulas (Table 4). The largest percentage difference in agreement was in favor of the Martin-Hopkins formula when LDL-D values were <55mg/dL (Friedewald's formula correctly classified 75.0% (95% CI 50.5-89.8) vs. the Martin-Hopkins formula which correctly classified 87.5% (95% CI 63.9-96.5) of subjects for this target). In the case of the other therapeutic targets, there was >90% agreement for both formulas. The kappa value showed “excellent” agreement (i.e., range 0.81-1) at levels <70, <100, and <116mg/dL for both formulas. In the <100mg/dL category, the highest value of κ=0.90 was obtained for the agreement between LDL-M and LDL-D. In all cases, agreement was statistically significant (p<0.001).
Agreement between calculated and direct cholesterol based on therapeutic targets for cardiovascular risk categories according to the European Society of Cardiology/European Atherosclerosis Society 20193 guidelines.
| LDL-F | LDL-M | |||||||
|---|---|---|---|---|---|---|---|---|
| LDL-D, mg/dL | F/Da | % (CI 95%) | κc | p-value | M/Db | % (CI 95%) | κc | p-value |
| <116 | 796/817 | 97,4 (96.1-98.3) | 0.89 | <0.001 | 795/817 | 97.3 (96.0-98.2) | 0.89 | <0.001 |
| <100 | 486/503 | 96.6 (94.7-97.9) | 0.88 | <0.001 | 491/503 | 97.6 (95.9-98.6) | 0.90 | <0.001 |
| <70 | 76/84 | 90.5 (82.3-95.1) | 0.81 | <0.001 | 77/84 | 91.7 (83.9-95.9) | 0.86 | <0.001 |
| <55 | 12/16 | 75.0 (50.5-89.8) | 0.53 | <0.001 | 14/16 | 87.5 (63.9-96.5) | 0.75 | <0.001 |
CLDL-D direct low-density lipoprotein cholesterol; LDL-F: low-density lipoprotein cholesterol calculated according to the Friedewald formula; LDL-M: low-density lipoprotein cholesterol calculated according to the Martin-Hopkins formula;
When we assessed the discordance between calculated and direct cholesterol for the very high- and high-risk therapeutic targets, LDL-F categorized 60.0% (n=18) of LDL-D cases >55mg/dL (n=30) as within the LDL target <55mg/dL and 29.0% (n=31) of LDL-D cases >70mg/dL (n=107) as within the LDL target <70mg/dL. For LDL-M the percentage of discordance was 36.4% (n=8/n=22) and 25.2% (n=26/n=103), respectively.
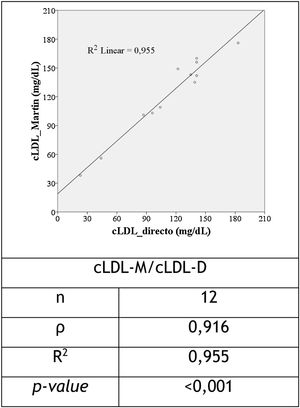
For the 12 cases in which Friedewald's formula was not applied (TG≥400mg/dL), the correlation between LDL-M and LDL-D was strong and statistically significant (ρ=0.916 and R2=0.955, p<0.001), as shown in Figure 3.
DiscussionLow-density lipoprotein cholesterol is a primary therapeutic target in the prevention of CVD.2–4 Accuracy is paramount to its detection. The reference method for LDL cholesterol measurement is expensive and labored in clinical practice. For simplicity, LDL cholesterol concentration has been estimated using the Friedewald formula in the last thirty years. It has more recently been called into question due to its lower accuracy in clinical situations such as hypertriglyceridemia and diabetes. The aim of this study was to apply a new formula using a variable TG:VLDL ratio (Appendix 1, Supplementary data) in a Portuguese population sample from the e_COR study, conducted by the Instituto Ricardo Jorge between 2012 and 2014.16 This new formula (named Martin-Hopkins) has shown superior accuracy to Friedewald's formula in several populations.11–13
In descriptive terms, the study sample has a similar gender prevalence (50.2% male and 49.8% female), aged between 18 and 79 years with a median of 51 (34) years of age, the median BMI corresponded to “overweight” in both sexes (BMI of 27.0 (5.7) kg/m2 in males and 25.8 (6.7) kg/m2 in females) and the median RFM15 was “obese” (RFM of 28.6 (6.6)% in males and 40.8 (8.2)% in females). RFM is a parameter that uses waist circumference instead of weight to define obesity, and its usefulness relative to BMI has been proven in several studies. Its cut-off points need to be validated according to the type of population/race.17,18
Regarding CVD risk factors, we found that almost half of the subjects had hypertension (48.5%). Obesity was present in 22.6% and diabetes in 11.7% of the sample, approaching the prevalence of diabetes recorded in the Portuguese population in 2021 of 12.9%19. However, the prevalence of diabetes in our sample was not adjusted to the Portuguese population, which according to the e_COR study report was 8.9% (95% CI: 7.5-10.3).16 More than a quarter of our sample was on statins (26.9%), which shows the wide use of these drugs in Portugal.20
The median LDL-D cholesterol was higher than the median of the estimated values (LDL-F and LDL-M) in the study population, with a statistically significant difference between medians for values calculated using the Friedewald formula of -3.1mg/dL (95% CI: -3.3 to -2.8, p<0.001) and for those calculated using the Martin-Hopkins formula of -2.8mg/dL (95% CI: -3.1 to -2.6, p<0.001), which despite a strong correlation coefficient, there were dissimilarities other than zero with respect to the direct measurement of LDL for both formulas. The differences found in the study population were lower than reported in other studies and in other populations.11,15 The median TG:VLDL ratio for the calculation of LDL-M was 4.8 (1.1), which is close to the values encountered by Sathiyakumar et al.,21 of 4.9 (4.3-5.7). Their study assessed the performance of the Martin-Hopkins formula vs. the Friedewald formula in a fasting and postprandial state and demonstrated the superiority of the Martin-Hopkins formula in both states. Compared to the study by Martin et al.,12 our ratio was lower than the reported 5.2 (4.5-6.0), as it is a factor that is dependent upon on the composition of the population under analysis. However, the described ratios are close to five, which explains the similarity in performance between formulas in the present and the previously mentioned studies, with superiority in all cases for the Martin-Hopkins formula.
According to previous studies, the trend in underestimations of LDL cholesterol when applying the Friedewald formula occurs mainly in the presence of diabetes, hypertriglyceridemia and LDL<70mg/dL.7,9,22,23In our study, we found a tendency for both formulas to underestimate LDL values in the study population and in the defined groups (Figure 1 and Table 3). The highest median LDL-D was in the group with hypertriglyceridemia (LDL-D of 131.0 (46.0) mg/dL), and in this group the most significant difference between median LDL-F and LDL-D of -9.0mg/dL was found (95% CI: -10.0 to -8.5, p<0.001). In the diabetes group, the difference between LDL-F and LDL-D values was also significant at -5.0 (95% CI: -6.0 to -4.0, p<0.001). Notably, LDL-M values were closer to LDL-D in these two groups: -2.2 (95% CI: -3.0 to -1.5, p<0.001) for the group with hypertriglyceridemia and -2.0 (95% CI: -2.8 to -1.3, p<0.001) for the group with diabetes. These results show the tendency of the Friedewald formula to underestimate LDL values when these conditions are present.. It is in in these clinical conditions that the Martin-Hopkins formula may be more useful.9,24,25
When we assessed Spearman's ρ correlation coefficients and linear regression according to group, we found that in all cases these values were higher when calculated with the Martin-Hopkins formula compared to the Friedewald formula, LDL-M values varied almost perfectly with LDL-D values in the groups no lipid-lowering therapy, no lipid-lowering therapy, obesity, diabetes, and hypertriglyceridemia, showing a strong correlation with LDL-D values (Figure 2). For LDL-F values, the correlation coefficients and linear regression also showed a strong approximation to the variation of the determined LDL-D values.
For LDL-D <70mg/dL, grade I therapeutic target and level of evidence A for individuals at high-risk of CVD3, described in other studies as one of the least accurate items calculated with the Friedewald formula,8,11,13,15,22,23 there was a weaker correlation compared with other groups for both formulas, with superiority for the Martin-Hopkins formula (Figure 2). The median LDL-M values in this group were very close to the median LDL-D, with a non-significant difference of -0.95 (95% CI: -2.1 to 0.2, p=0.117), showing the superiority of the Martin-Hopkins formula in this range of values. This has also been validated in other studies.11,13,21,24
Regarding the agreement between LDL-M cholesterol and LDL-F cholesterol and the LDL-D values established by the ESC/EAS 20193 as recommended therapeutic targets, accuracy was lower as the LDL-D value decreased for both formulas. However, superiority was found for the Martin-Hopkins formula at the first three targets (LDL-D <55, <70, <100mg/dL) and the highest value of κ=0.90 for LDL-M when LDL-D <100mg/dL, which may allow for greater confidence when assessing the lipid profile of very high-, high-, and moderate risk individuals, in whom these targets are important goals. These findings are in line with what original study outcomes and in a population-based validation study of this formula.12,13 Regarding <116mg/dL values, as found in another study,15 LDL-F was marginally more in agreement compared with LDL-M, 97.4% (95% CI: 96.1-98.3% vs. 97.3% (95% CI: 96.0-98.2%).
When we assessed the discordance between the calculated values and LDL-D, according to the Friedewald formula, 60.0% and 29.0% of the subjects were within the therapeutic target of very high and high-risk, which would hypothetically imply less therapeutic optimization in these cases. In the case of the Martin-Hopkins formula, smaller discrepancies were found, whichare corroborated by other studies.26,27 In the studies by Palmer et al.26 and Martin et al.27, the new formula lead to a higher estimate of LDL cholesterol values compared to the Friedewald formula, particularly in patients with low LDL cholesterol levels. It was suggested that the Martin-Hopkins method may prevent undertreatment due to the underestimation of LDL using the Friedewald method for this range of values.
Although the group of individuals with TG greater than or equal to 400mg/dL (n=12) was small, the ρ and R2 coefficient were strong (>0.9) and significant (p<0.001). These results were not observed by Palmer et al.,26 who found the new method of calculating LDL to be inaccurate in patients with TG≥400mg/dL when compared to LDL cholesterol measurement using β quantification, however further studies will be needed to prove these data.
In summary, higher correlation and linear regression coefficients, higher agreement and smaller differences between LDL-M and LDL-D values compared to LDL-F values were encountered, especially in the groups with diabetes, hypertriglyceridemia, LDL-D <70 and <100mg/dL. It is clear that the use of this new formula to estimate LDL is an improvement on the more widely used Friedewald formula. As described by Martin et al.,12 changing a calculation is a simple matter in a modern laboratory and can be easily incorporated into automated laboratory reporting systems at virtually no additional cost. The 180 stratified cells (Appendix 1, Supplementary data) can be added using online software (http://ldlcalculator.com/) and thus easily implemented in most clinical laboratories. Although it is a formula that involves consulting a table for the TG variable divisor, in clinical practice there is the possibility of using a mobile application developed by the Ciccarone Center for Cardiovascular Disease Prevention at Johns Hopkins Hospital which estimates LDL cholesterol using the Martin-Hopkins method (https://www.hopkinsmedicine.org/apps/all-apps/ldlcholesterol-calculator).
It is also important to note that LDL cholesterol in clinical practice is a unique component among many of the factors that determine an individual's risk of CVD.1–4 Using other parameters such as non-HDL-cholesterol as a therapeutic target means interferences in the calculation of LDL can be minimized when making treatment decisions. This is particularly recommended in people with high TG, diabetes, obesity, or very low LDL levels (grade I recommendation, level C)3,24.
LimitationsOne limitation of this study was the method for direct measurement of LDL cholesterol, which was not the same as that applied by Martin et al.12, who used direct ultracentrifugation with vertical automatic profiling (Atherotech) and by Friedewald et al.6, who used β-quantification. However, direct methods (3rd generation homogeneous assays) for LDL cholesterol measurement showed good reproducibility and were certified by the Cholesterol Reference Methods Laboratory Network of the Centers for Disease Control and Prevention.28
In the present study, single measurements were assessed, so they do not take into account individual variation in lipid levels.
StrengthsIt is the first study in the Portuguese population that shows the applicability of the Martin-Hopkins formula in relation to the Friedewald formula, which is widely used in Portugal.
ConclusionThe strength of this study is lies in the fact that it is the first study in the Portuguese population to show the applicability of the Martin-Hopkins formula in relation to the Friedewald formula, which is widely used in Portugal. The formula developed by Martin et al.12 uses an adjustable factor for the TG/VLDL ratio, which leads to superior accuracy than the more commonly used Friedewald formula for estimating LDL concentration. The application of this new formula is simple and valid in our sample; it shows superiority over the Friedewald formula, especially for LDL-D values <100mg/dL and in the diabetes and hypertriglyceridemia groups.
FinancingThis research has not received any specific funding from any commercial, public, or non-profit sector.
Declaration of interestThe authors declare that there is no conflict of interest that could be perceived as detrimental to the impartiality of the reported research.
AcknowledgmentsThe authors would like to thank the subjects, researchers, and analytical technicians who worked on the e_COR study research project.
Please cite this article as: Ferrinho C, Alves AC, Bourbon M, Duarte S. Aplicabilidade da fórmula Martin-Hopkins e comparação com a fórmula Friedewald na estimativa do colesterol LDL na população do estudo e_COR. Rev Port Cardiol. 2021;40:715–724.